|
|
|
The loci of phase-matching directions for biaxial crystals.
(Program Set LID-FC)
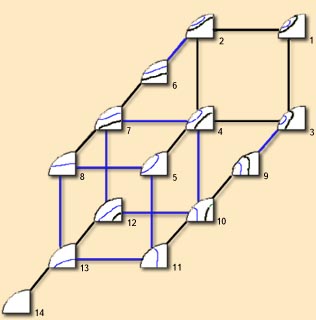 |
In 1967 was designed the loci of phase-matching directions for biaxial crystals (classification diagram) by M.V.Hobden (J.App.Phys., 38, 4365 (1967)) .
The comparison analysis of biaxial crystals with applications of LID-FC shows that Hobden's phase matching direction diagram is not complete.
|
|
Also there are two add configurations for phase-matching directions. For second type of interaction (SFF type) phase matching can take place along X axis.
Complete diagram has the following form. |
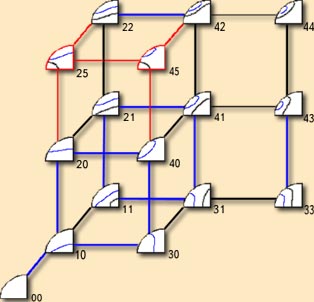 |
What can give complete classification? All crystals may be classified in acording this diagram and define wavelengths when transient from one to other element of diagram can take place. At these wavelength the phase-matching direction is along one of optical axis of crystal. In this case the angular phase-matching width is maximal (angular noncritical phase matching).
Character of transients allows us to define the spectral band for spectral noncritical interactions. In these band the second harmonic generation for femtosecond pulses is possible. Also is is possible obtain second harmonic generation for tunable laser radiation.
More detail:
Proceedings of SPIE, v.3733, p.228-236.
Quantum Electronics (Rus.), 2000, v.30, N5, p.377-386.
For example, below presented table contains wavelength, at which take place the transient on phase-matching diagram for three crystals of mm2 point group of symmetry - KTP, CTA è KTA. For these crystals the maximal value of nonlinear efficiency coefficient is for second type of interaction - SFF (for all main planes of crystal).
For KTP crystal the second harmonic generation on SFF type is possible from 993,9 nm to 3105,5 nm.
On the wavelength 993,9 nm, 1079,5 nm and 3105,5 nm are realized angular noncritical phase matching.
In the band from 1079,5 nm to 2981,7 nm the wavelength noncritical interaction take place.
|
| | | | | | | |
| Diagram |
Element - Transient |
KTP - SSF |
KTP - SFF |
CTA - SSF |
CTA - SFF |
KTA - SSF |
KTA - SFF |
 |
00 |
700 |
--- |
700 |
--- |
700 |
--- |
 |
00-10 |
741 |
--- |
900,8 |
--- |
771 |
--- |
 |
10 |
--- |
--- |
--- |
--- |
--- |
--- |
 |
10-20 |
796,2 |
--- |
1023 |
--- |
842,8 |
--- |
 |
20 |
--- |
--- |
--- |
--- |
--- |
--- |
 |
20-21 |
--- |
993,9 |
--- |
1280 |
--- |
1034,7 |
 |
21 |
--- |
--- |
--- |
--- |
--- |
--- |
 |
21-22 |
--- |
1079,5 |
--- |
1548 |
--- |
1147,7 |
 |
22 |
--- |
--- |
--- |
--- |
--- |
--- |
 |
22-21 |
--- |
2981,7 |
--- |
2371 |
--- |
2947 |
 |
21 |
--- |
--- |
--- |
--- |
--- |
--- |
 |
21-20 |
--- |
3105,5 |
--- |
2947 |
--- |
3448 |
 |
20 |
--- |
--- |
--- |
--- |
--- |
--- |
 |
20-10 |
4054 |
--- |
3697 |
--- |
4547,7 |
--- |
 |
10 |
--- |
--- |
--- |
--- |
--- |
--- |
 |
10-00 |
4251 |
--- |
4244 |
--- |
4701,7 |
--- |
 |
00 |
4500 |
--- |
5300 |
--- |
5300 |
--- |
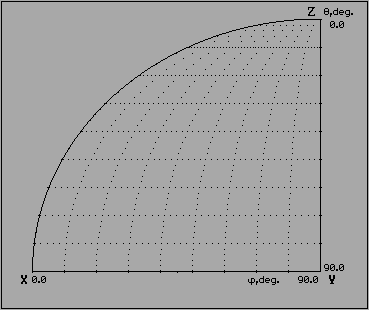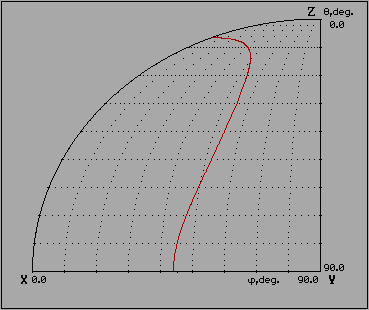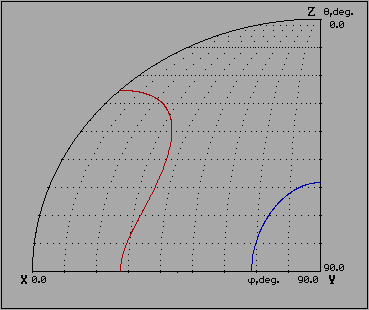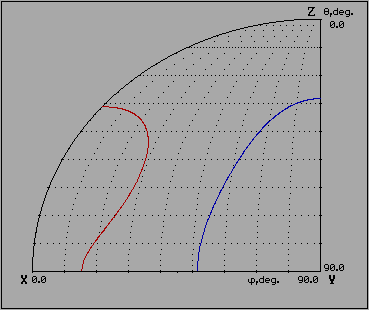
This picture shows dinamic of transients for LBO crystal versus wavelgth of fundamental radiation.
|




















